一、面的基础考法

数个数

若题干白色窟窿较多，优先考虑数面

有的题目中，点和面的特征图比较像。在考场上，建议优先数面，因为面更好数

（2019 青海）

【解析】本题白色窟窿较多，优先考虑数面。题干图形面的数量依次为 1、2、3、4、5，则“？”处要选择有 6 个面的图形。只有 C 项有 6 个面，选择 C 项。【选 C】 

二、面的细化考法

当题干特别符合数面特征图（出现很多白色窟窿），但数面选不出唯一答案，考虑面的细化： 

（1）三角形（考查较多）、四边形的面（很少考）

（2）相同面（形状和大小都一样）的个数

（3）最大面/最小面的属性（轴对称/中心对称、曲线/直线）、形状（四边形/三角形）

先考虑面的细化，若无规律，再考虑数点

（2018 广州）

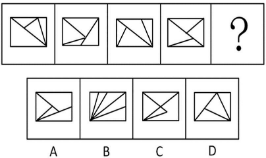
【解析】本题白色窟窿较多，优先数面，题干图形都是 4 个面。B 项有 5个面，排除；A、C、D 项均有 4 个面，保留。 考虑面的细化，先看是否有三角形面。题干每幅图中所有的面都是三角形，则“？”处所有的面也应为三角形。 A 项：上面出现四边形，排除。 C 项：右下角出现多边形，排除。 B 项：虽然所有的面都是三角形，但是有 5 个面，个数不符合，排除。【选 D】 

（2018 黑龙江）

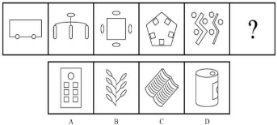
【解析】本题白色窟窿较多，优先考虑数面。整体数面，数量依次为 3、4、5、6、8，整体数无规律，考虑细化。本题没有三角形面，但出现形状、大小都相同的面，数相同面的个数。图 1 出现“车轱辘”，相同面有 2 个；图 2 类似“烛台”，相同面有 3 个；图 3 相同面有 4 个（椭圆），图 4 相同面有 5 个（方框），图 5 有 6 个相同面（小星星），则“？”处选择有 7 个相同面的图形，选择 B 项。【选 B】 

【注意】本题涉及的考点并不难。当一个图形有很多相同面时，直观的视觉感受是不一样的，形状、大小都一样，能想到数相同面的个数。 

（2017 河南）

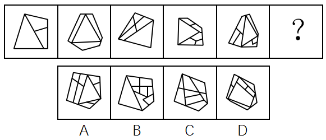
【解析】本题出现很多白色窟窿，优先数面。题干图形面的数量依次为

3、4、5、6、7，则“？”处要选择有 8 个面的图形。A 项有 9 个面，排除；B、C、D 项均有 8 个面，无法排除，选不出唯一答案。 考虑面的细化。题干每幅图均有很多三角形面，但 B、C、D 项也有很多三角形面。本题最大面很特殊，每幅图最大面的形状均为三角形。 B 项：最大面为三角形，当选。 C 项：最大面是四边形，排除。 D 项：最大面是梯形，排除。【选 B】 

（2019 事业单位）

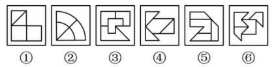
【解析】本题出现很多白色窟窿，优先数面。每幅图都是 4 个面，无法两两分类。整体数面无规律，考虑面的细化。本题没有三角形、四边形面，但有相同形状的面。图 1 中，左上方的两个三角形面相同，下方的两个正方形面相同，则相同面有 2 对；图 2 相同面有 2 对，图 3 有 3 个相同面，图 4、图 5 有 3 个相同面。因此，图③④⑤为一组，有 3 个相同面；图①②⑥为一组，有 2 对相同面

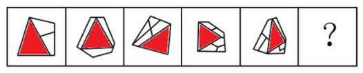
（2019 江苏）

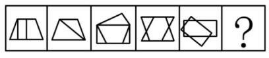
【解析】2019 江苏：本题出现很多白色窟窿，优先数面，选不出唯一答案。考虑面的细化，先看是否有三角形面。题干三角形面的个数依次为 1、2、3、4、5，则“？”处要选择有 6 个三角形的面

（2018 事业单位）

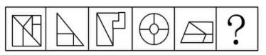
【解析】白色窟窿较多，但数面选不出唯一答案，考虑面的细化。图 4 没有三角形面，也没有四边形面；图 2 中没有形状、大小相同的面。考虑最大/最小面，本题考查最小面（概率小），最小面与外框形状一致。图 1 最小面是正方形，与外框形状一致；图 2 最小面是直角三角形，与外框形状一致；图 4 最小面是圆圈，外框也是圆圈，二者一致。因此，“？”处图形的最小面也应与外框形状保持一致。