一、对称的基础考法

区分轴对称和中心对称

对称轴的数量、方向

出现等腰元素，考虑轴对称。等腰即左右一样、上下一样，图形很规整

出现平行四边形、以及“S、Z、N”的变形图，考虑中心对称

若一个图形包含两条相互垂直的对称轴，考虑既轴又中心对称

命题趋势：基本特征图的变形。对称性的难点在于无法识别特征图。如果是直角三角形、明显的等腰元素，难不住大家，因此命题人会把基础图形变形考查

大风车”一类的图案多是中心对称

“相同图形”反方向放多是中心对称 

【解析】图形各异，考虑数量和属性类。图中所有图形都是对称，考虑对称性。题干所有图形都是纵轴对称【选 A】

（2020 北京）

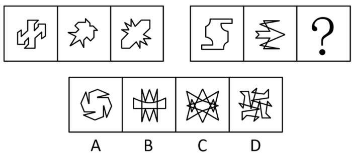
【解析】第一组图 1、A 项、D 项均是“风车”，优先考虑中心对称。第一组图，图 1 是中心对称，图 2 是轴对称，图 3 有两条相互垂直的对称轴，为“轴+中心对称”；第二组图，图 1 是中心对称，图 2 是轴对称，则“？”处应为“轴+中心对称”。只有 C 项既是轴对称又是中心对称图形（有两条相互垂直的对称轴），选择 C 项。【选 C】 

（2019 山东）

【解析】D 项为五角星，可以看笔画数，但同时五角星也是对称性的特征图。若既符合对称，又可以看笔画，优先看对称（笔画不好数，哪个简单先看哪个）。画出对称轴，确定方向、条数。第一行，图 1 关于竖轴对称，图 2 关于横轴对称，图 3 有横竖两条对称轴；第二行，图 1 关于竖轴对称，图 2 有横竖两条对称轴，图 3 有三条对称轴（等边三角形）；第三行，图 1 有横竖两条对称轴；图 2 有三条对称轴（等边三角形）。 

第一行对称轴数量依次为 1、1、2，1+1=2；第二行对称轴数量依次为 1、2、3，1+2=3；第三行对称轴数量依次为 2、3、？，则“？”处对称轴数量应为 5（2+3=5），选择 D 项。【选 D】 

二、轴对称的延伸考法

                                          图一

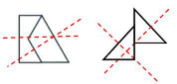
                                      图二

对称轴与图形的关系

高频考点是对称轴与线的关系。比如图一中，图 1 对称轴与原图线条重合，图 2 对称轴与原图线条垂直，图 3 对称轴与原图线条平行

对称轴与点的关系。比如图一中，图 3 对称轴穿过原图的 2 个交点

对称轴与面的关系。比如图一中，图 4 中间的竖线是对称轴，对称轴左右两侧出现一模一样的两个图形，即对称轴左右两侧有相同的面

当有多个等腰图形拼合在一起（图形之间以线相连），考虑对称轴之间的关系（平行、相交、垂直）。比如图二中，图 1 左侧图形是水平对称轴，右侧是一个等腰梯形，关于“右上-左下”方向的斜轴对称，两条对称轴的夹角为 45°；图 2 的两条对称轴互相垂直

（2018 北京）

【解析】图 1 类似“箭头”（等腰元素），图 2 出现等腰三角形。出现很多等腰元素，优先画出对称轴。观察发现，每幅图形均只有 1 条对称轴。 

A 项：有 2 条对称轴，排除。 B 项：没有对称轴，排除。 C、D 项均有 1 条对称轴，无法选出唯一答案。考虑对称性的延伸考点，看对称轴与线、点之间是否有关系。观察发现，每幅图的对称轴均与原图的一条线重合。 

C 项：对称轴不与任何线条重合，排除。 D 项：对称轴与原图“左上-右下”方向的线条重合，当选。【选 D】 

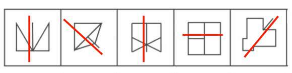
【注意】当每幅图有且只有 1 条对称轴，而且方向无规律，考虑对称轴是否与线重合、平行、垂直或者穿过某个点。 

（2020 国考）

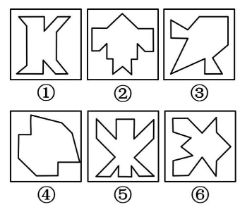
A ①③④，②⑤⑥ 

B ①②⑥，③④⑤ 

C ①④⑤，②③⑥ 

D ①④⑥，②③⑤

【解析】题干出现等腰元素，画出对称轴。若看对称轴方向，图①关于横轴对称，图②关于竖轴对称，图③关于斜轴对称，方向无法两两分类，且每幅图均只有 1 条对称轴，考虑对称轴与线、点、面之间的关系。图①的对称轴与外框的两条线垂直，图②的对称轴穿过 2 个交点，图③的对称轴穿过 2 个交点，图④的对称轴与外框的两条线垂直，图⑤的对称轴与外框的两条线垂直，图⑥的对称轴穿过 2 个交点。因此，图①④⑤为一组，对称轴均与外框的两条线垂直；图②③⑥为一组，对称轴均穿过 2 个交点，选择 C 项。【选 C】 

（2020 广东选调）

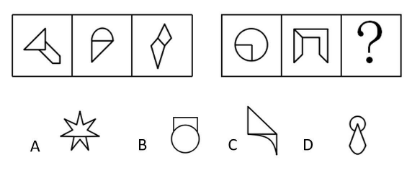
【解析】题干每幅图均是图形与图形拼在一起（以线相连），而四个选项均相交于线。观察发现，每幅图均由两个具有等腰元素的图形组成，画出每幅图的两条对称轴，看对称轴之间的关系。第一组图，图 1 的两条对称轴重合，图 2的两条对称轴呈 45°夹角，图 3 的两条对称轴平行；第二组图，图 1 的两条对称轴重合，图 2 的两条对称轴呈 45°夹角，则“？”处的两条对称轴应平行。 C 项：两条对称轴平行，当选。 A、B、D 项的两条对称轴均重合，均排除。【选 C】 

【注意】图形由两个具有“等腰”元素的图组成，考虑拆开看

（2019 联考）

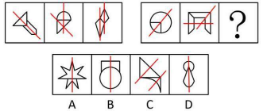
【解析】每幅图都是外部有一个圆圈、内部有一个图形，而且内部有一条线。内部的线条依次顺时针移动，则“？”处的直线应在左下角，排除 B、C 项，剩余 A、D 项。观察发现，A、D 项内部均出现等腰元素，考虑对称。画出对称轴，对称轴方向依次为竖轴、横轴、竖轴、横轴、竖轴，交替出现，则“？”处对称轴的方向应为横轴。 A 项：对称轴的方向为竖轴，排除。 D 项：对称轴的方向为横轴，当选。【选 D】 

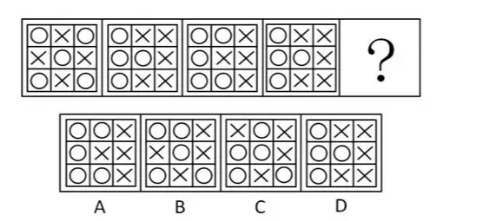
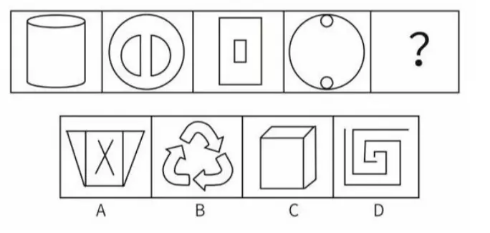
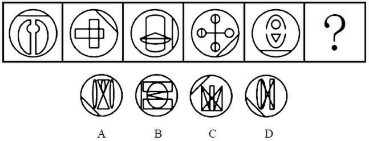
【解析】题干都是对称图形，排除 BC。题干圆形得数量 5、4、5、4、？，则选项应该有 5 个圆【选 A】

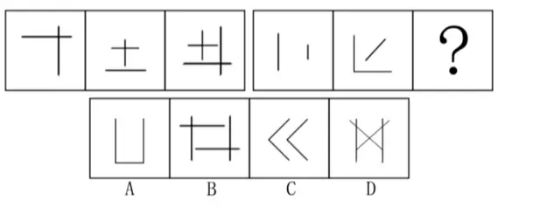
【解析】234条直线，排除A。对称轴逆时针旋转【选 D】