一、二进制

在计算机中，数字是采用二进制表示的，在大部分开发语言中，通常使用 8 位、32 位、64 位二进制来表达数字

不同位数二进制可以表示的数字数量：一个二进制位可以有 1 和 0 两种取值，我们令用来表示数字的二进制位数为 n，那么可以表示的数字数量就是 2 的 n 次方个，如使用 8 位二进制来表示数字，那么可以表示的数字数量为：2 的 8 次方 = 256 个

二、区分正负

数字有正负之分，通常采用最高位为符号位，表示一个二进制串所表示的数字正负，最高位为 1 时数字是负数，最高位为 0 时数字是正数或 0

具体的表示例子：以八位二进制为例，将八个二进制位从右往左编号，如下：

0 0 0 0 0 0 0 0
8 7 6 5 4 3 2 1

正数表示，编号为 8 的最高位取值 0

编号为 1 的二进制位取值为 1 时，表示 2^0 = 1

编号位 2 的二进制位取值为 1 时，表示 2^1 = 2

编号为 3 的二进制位取值为 1 时，表示 2^2 = 4

………………

编号为 7 的二进制位取值为1时，表示 2^7 = 64

当我们想要表示一个数字时，就可以将对应的二进制位取值为 1，然后相加即可，如：5 = 4 + 1 = 00000101 

由此也可以得出 8 位的二进制位所能表示的最大数字为：64+16+8+4+2+1 = 127

负数表示，编号为 8 的最高位取值为 1

三、补码

有关负数的表示较为复杂，这是因为负数涉及到减法运算导致的，在计算机的设计中，为了节省资源，只有加法运算器而没有减法运算器，而减法运算可以通过加上一个负数的方式进行；

那么负数应该如何表示呢？假设我们只将最高位设为 1，其他位数的表示规则和正数一致，能否正确运算减法呢？可以做一个实验确认，假设要运算 6-4，那么运算过程如下： 6 = 00000110，-4 = 10000100，将二者按位相加，那么：

6 - 4 = 6 + (-4) = 00000110 + 10000100 = 10001010 = -10

很明显出现了问题，运算出错，于是乎就有了补码的出现用来表示负数解决该问题

四、取模

补码是通过取模的方式来表示负数的，什么是模呢？我们在玩游戏的时候当有某个职业或者某把武器数值过高，非常强时，就会说这个东西”超模“了，因此模可以理解为一个上限；

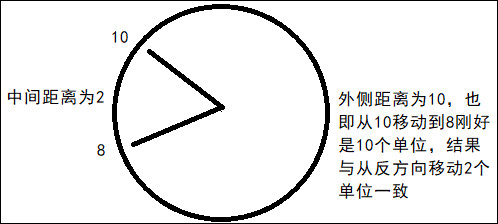
再从一个日常例子入手，12 小时制的时钟，每过 12 点就会从 0 开始重新计算，此时的 12 就是一个模，对 12 取模可以将大于 12 的数表示成 [0,11]之间的数，如：13 % 12 = 1，那么假设现在是 10 点，我们想要知道两个小时前的时间，这就涉及到了减法：

10 - 2 = 8

而如果引入取模，那么还可以表示成：

(10 + 10) % 12 = 8

换句话说，我们可以通过取模的方式用一个正数去代表负数，那么这个正数应该如何取呢？留意到模为12，而 12 = 10 + 2，也即一个负数的绝对值与代表该负数的正数之和刚好为模，原因如图：

在二进制中，负数也就是用取模的方式来表示的，在不考虑符号位的情况下，仅以二进制串来表示正数时，其取值范围是：[0，2^n- 1]，n 是二进制位数，当二进制位均取 0 时表示 0，均取 1 时表示 2n- 1；

而 2^n - 1 + 1 = 2^n，需要一个更高位的 1 来表示，此时位数越界，现有二进制位清 0，所以 2^n 天生适合作为模

五、减法

解决了模的问题后，就可以解决减法问题了，假设要计算 a - b，模为 2^n，n 为二进制位数，那么就可以表示成 a + (2^n - b)，将 b 按位取反，用 ~b 表示，由 b + ~b 的结果是各二进制位都为 1，可得：

b + ~b = 2^n - 1，即：2^n - b = ~b + 1

于是 a + (2^n - b) 可以表示为：a + ~b + 1，也即 -b 可以用 ~b + 1表示，到这里，负数的表示也就可以明确了，步骤如下：

• 首先取得该负数的绝对值 |b|，为正数

• 接着对该绝对值按位取反再加 1，即 ~|b| + 1

• 由于正数和 0 的最高位是 0，取反后为 1，所以负数的最高符号位都为 1

最后需要明确的是，负数的取值之所以如此曲折，是为了解决减法的问题，而将正数的最高位规定为 0后，运算后得到的负数二进制表示最高位也恰好为 1，可用于区分正负，不得不感叹前人智慧